The July 2022 Mathcad Community Challenge on the PTC Community site was another geometry problem:
Given the following three points on a circle of radius 10 units, calculate the area of the spherical triangle:
(5.339, 6.948, 4.819)
(-4.018, -3.703, 8.375)
(6.455, -6.679, -3.705)
(Note that the point coordinates are rounded to three decimal places.)
Optional
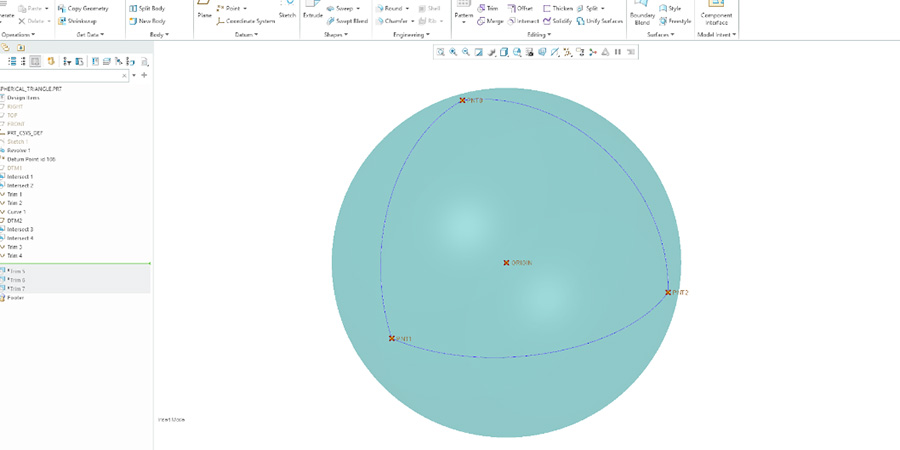
I generated the points using a part model of a sphere in Creo Parametric. With some construction geometry, I was able to trim to the spherical triangle. The area measurement function in Creo came up with a value of 246.72 square millimeters.
Let’s take a look at the qualifying submissions.
Username “ppal” was the first to respond, noting that the numbers in the original post indicated a circle not located at the model origin. Yikes! I had written down the coordinates of the second point incorrectly.
Ppal submitted a couple worksheets. Referencing Folke Eriksson’s “On the Measure of Solid Angles,” they created vectors for the three points and solved quickly and easily for the area. Nice research! I also like the documentation, use of an image, and color applied to text regions.
A second submitted worksheet defined a function that calculates the spherical triangle using inputs of three point vectors and the circle radius. The use of vectors makes the function elegant.

As usual, Terry Hendicott was the first to submit a worksheet. Actually, he submitted multiple worksheets, solving for both the incorrect initial numbers as well as the corrected coordinates!
If you have not checked out Terry’s worksheets from previous challenges, I recommend you check those out as well as this month’s. His worksheets are always beautiful, making great use of text, images, color, and highlighting.

One worksheet used Girard’s Theorem, which calculates the angles of the great circles between the three points, and using the “excess” (the sum of those angles minus pi radians) to calculate the area. He also solved the first optional problem of writing a program that calculated the area as well.
Another worksheet used L’Hillier’s Theorem, which is a really long formula. Even in landscape mode, you have to view the worksheet in Draft mode. Since much of the formula appears under a square root, I don’t think you can use one of the Equation Break operators introduced in Mathcad Prime 4.
One of Terry’s earlier worksheets used an even longer version of L’Hillier’s Theorem to account for the incorrect coordinates I initially gave. It used symbolic evaluation with the solve keyword to calculate the origin of the sphere.
Terry also built on ppal’s work by using ppal’s formula to solve for the area via symbolic evaluation, which was the second optional challenge. Excellent teamwork! That’s what we like to see in these challenges: people using the power of community to build upon each other’s work.
First-time challenger Johan Eppinga used a Solve Block to determine the center of the sphere and verified it was at the origin. (I love the use of Solve Blocks in this worksheet. Solve Blocks are my favorite construct in Mathcad.)
Then he calculated the distance and angles between points. With the three angles, you can determine the Spherical Excess, which can be used in a formula to determine the area.
For some reason, the area calculation was incorrect. I encourage a user to check their work to determine the error. (The calculation of the angles appears to be incorrect.) Nice worksheet, though.
Once again, we had multiple submissions that took different approaches to the solution. Do you want to level up your Mathcad skills? I don’t think you’ll find a faster approach than looking at how some Mathcad experts tackle these challenges.
Stay tuned for the September challenge, which will be an electrical engineering problem! Subscribe to the PTC Mathcad Community Challenge Index and Guidelines thread on the PTC Community for when that challenge will be up, as well as links to the other challenges and their blog articles.
You'll know whenever there is a new Mathcad Community Challenge, plus other Mathcad tips, tricks, and more!