Most of the calculations we deal with every day require us to find the roots of a function. For example, to minimize a function, you have to find the root of its derivative. Do you know how Mathcad can help you find the roots you’re looking for?

In today’s post I’ll discuss three worksheets that demonstrate some of Mathcad’s built-in functions dedicated to root finding.
The first worksheet provides examples of how to find roots algorithmically by using Mathcad’s root function. (Note that this function only solves one equation with one unknown.) You can call the root function with either two or four arguments, depending on whether you wish to provide a guess value for the root above the function call, or bracket values for the root within the function call.
For functions with complex roots, you can also use complex guess values to find a complex root of the function.

Example of how to use the root function
You can use the root function to extract the roots of a polynomial one at a time, but it is often more convenient to find all the roots at once, using the function polyroots. This function returns a vector containing the roots of the polynomial. The input to polyroots is a single vector of real or complex numbers containing the coefficients of a polynomial. The coefficients are listed from lowest degree to highest, including all 0 coefficients.

Example of how to define the coefficient vector and how to find the roots vector.
If the roots of a polynomial are not distinct, you can read the “Repeated and Paired Roots” section from the worksheet to see how Mathcad handles this situation.
I’m sure you are aware that Mathcad has two types of mathematical engines: numeric and symbolic. You can use the symbolic processor in Mathcad to find roots symbolically. This may be more accurate than numerical root finding, and can also yield more information about a solution.
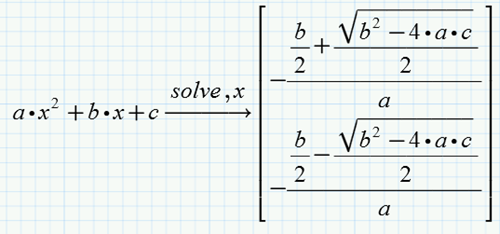
Simple example of symbolic root finding
You can assign the symbolic solution to a variable or a function, making it available for use in the worksheet. When there is more than one solution, such as in the quadratic equation above, the solution is stored within a vector, where each element represents one part of the overall solution.
Also note that since the expression contains several variables, you must type a comma after "solve," followed by the variable, x, for which you are solving.
You can find these three worksheets, and many more in-depth examples, in the PTC Mathcad Worksheet Library – Education collection at the PTC Webstore.