
Galileo Galilei reportedly said, “Mathematics is the language with which God has written the universe.” Since then, people have spoken variations of this statement like “math is the language of physics.”
The language of mathematics is beautiful and has repeating motifs that speak to underlying symmetries. One of these patterns is the quadratic form for equations found in geometry, motion, magnetism, energy, and other fields. Here are some of those equations documented in PTC Mathcad:

The quadratic form is an equation in which the highest exponent of a variable is two – the square of that variable. Here, all the equations have the form one-half times a variable for a property times the square of a measured quantity. Why is this?
I was re-reading "The Tau Manifesto" when I was reminded why this motif exists. Let’s start with a basic example: free fall.
Suppose an object at rest (initially velocity zero) then falls under the effect of gravity. From the equations of motion for constant acceleration, the velocity v is the product of the acceleration due to gravity (g) multiplied by the time (t):
v=g·t
We can graph and format the velocity as a function of time using Mathcad’s Chart Component functionality:
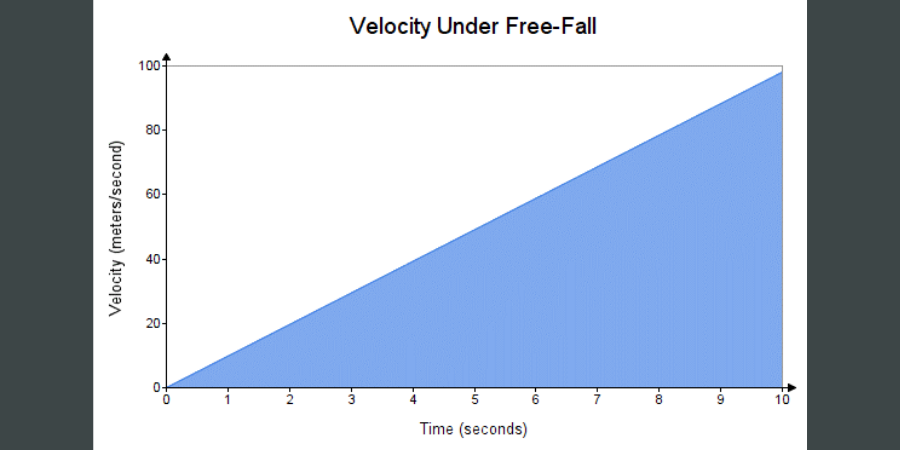
The area under the curve is shaded. That is the product of velocity and time, which yields another useful quantity: the distance traveled. We have connected acceleration to velocity to distance.
Calculating the area under the curve is so useful in so many fields that it led to the simultaneous development of a new form of math by Sir Isaac Newton and Gottfried Wilhelm Leibniz: calculus. (Finding the area under a curve is integral calculus.).
In this situation, the area under the curve is a triangle. The area of a triangle is equal to one half the base times the height. Here, the base is time, and the height is the velocity, which is the acceleration due to gravity times time (g · t). Therefore, the area under the curve, the distance traveled, is: ∆x=1/2· g · t2
The area under the curve yields the quadratic form. We can also derive these quadratic forms using Mathcad’s built-in integral calculus operators and symbolic evaluation:

In his Second Law of Motion, written in 1686, Sir Isaac Newton defined force as the product of an object’s mass times its acceleration. This was one of the greatest breakthroughs in the history of physics.
Then in 1802, Thomas Young first used the term “energy” to describe a quantity related to mass times the square of velocity. Later, the math behind the concept of energy would equate it to work, which is force exerted over a distance.
Like our example with acceleration and velocity, we could graph force and distance to calculate energy. To solve this mathematically involves derivations that take leaps of brilliance. We can document these derivations in Mathcad as well:

Calculus links force to energy, once again expressed in the beautiful quadratic form.
We can repeat these techniques of symbolic evaluation formulas like area of a circle and the potential energy in a spring. We can use derivations to arrive at formulas for rotational kinetic energy and the energy stored by induction in a magnetic field. Both techniques allow us to describe the universe with quadratic forms of equations from calculus.
Mathcad helps you understand and express the language of physics. If you want to explore Mathcad’s capabilities for calculus, symbolic evaluation, documentation, and chart creation, download Mathcad Express for free today.
Perform, analyze, document, and share your calculations starting now!