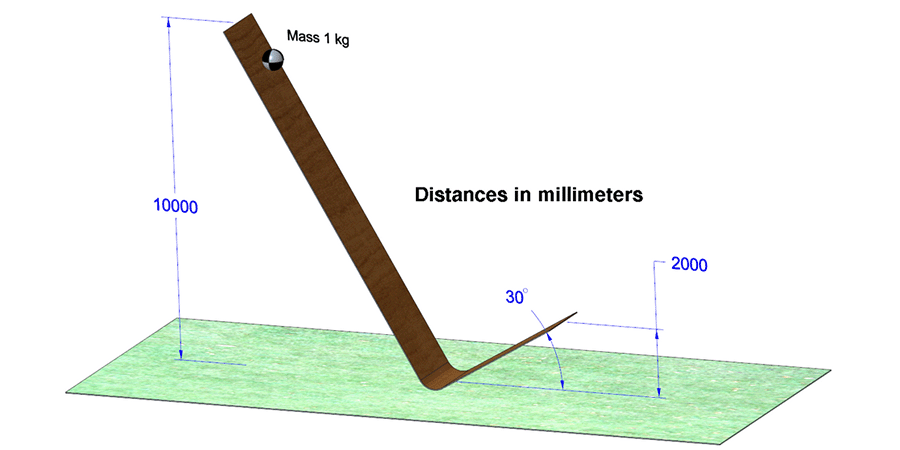
The Mathcad Community Challenge for May 2023 was as follows:
A ball with a mass of 1 kilogram is at the top of a frictionless ramp 10 meters above the ground. The ball rolls down the incline and launches from a height of 2 meters and an angle of 30 degrees above the ground.
The problems to be solved are:
Frequent contributor PPal submitted the first and multiple worksheets. I like that they build on previous worksheets. I hadn’t intended people to take moment of inertia into account, but PPal did. Functionality in the solutions included user-defined functions, symbolic evaluation, the polyroots function, XY plots, and 3D plots. The worksheets incorporated multiple aspects to make the worksheet friendly to others, including text with different fonts, images, and highlighting.
Fred Kohlhepp, another loyal contributor, submitted an attractive Mathcad Express worksheet with numerous XY plots that greatly help to convey information to the reader. Fred also uses another technique I like: documenting the thinking behind your equations using the equality comparison operator (the thick equals sign). Fred also figured out the trick behind question 4. Since the acceleration due to gravity falls out of the equations, the horizontal distance is the same on the Earth, Moon, or any planetary body.
Jeff Henning’s submission wins the award for the most publication-ready worksheet. It could be used to teach physics to high school and college students. Jeff uses collapsible areas to organize the worksheet into assumptions, derivations, inputs, function definitions, and the answers to each question. Jeff gets extra points for being the first person since the challenge started to use the Chart Component. He plots the trajectory of the ball as well as the distance versus launch ramp angle. The 3D Plot for question 6 is also beautifully formatted. Another small thing that makes a huge difference: Jeff uses the document footer including page numbers. Just a beautiful work of art.
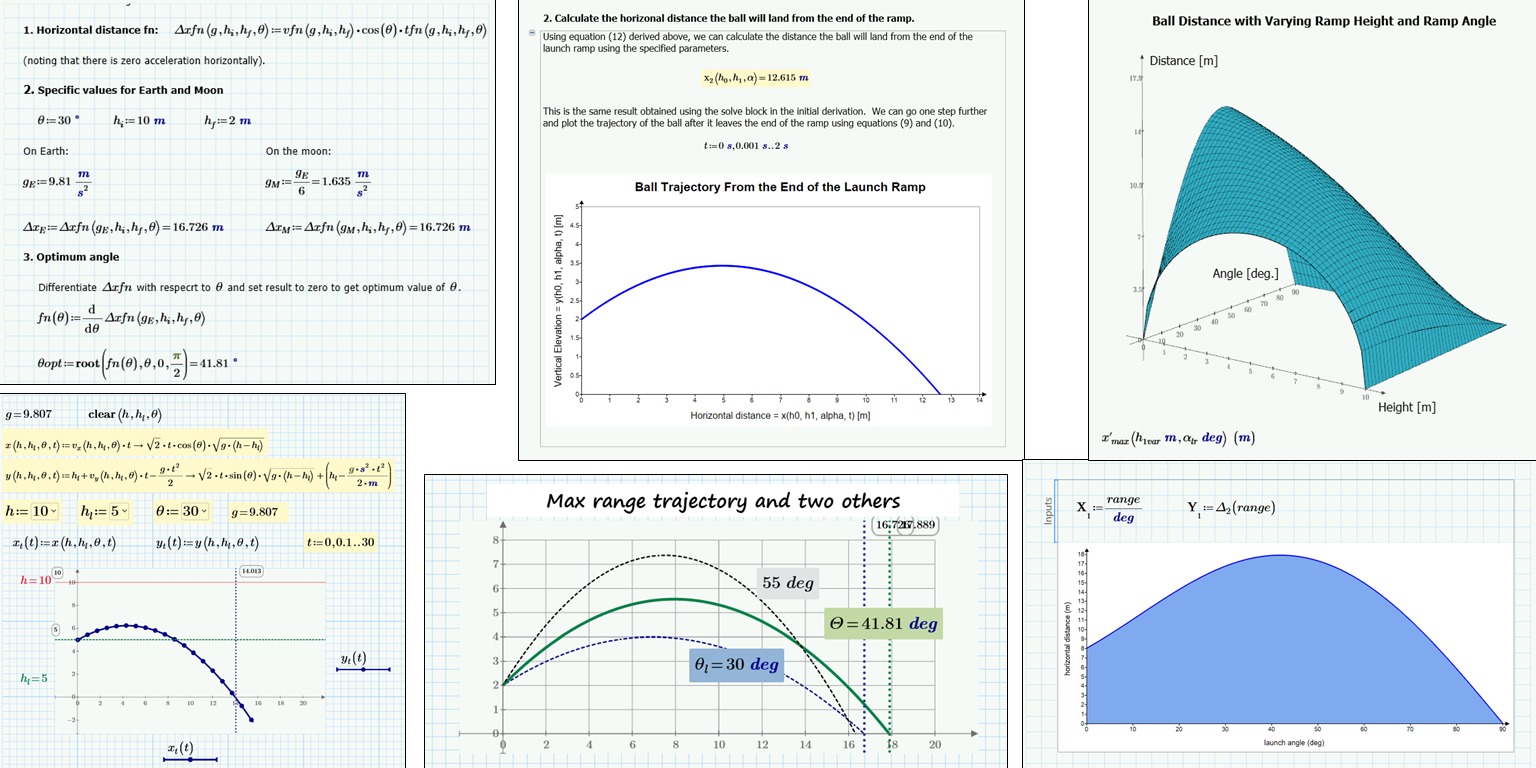
A collage of the different entrants' Mathcad Prime worksheets.
Be sure to download and check out the sheets for yourself!
As usual, TTokoro submitted an inviting worksheet complemented with text, highlighting, XY Plots, 3D Plots, and headers and footers. Draft View was used to hide some calculations, which helps keep worksheets neat. The math made heavy use of symbolic evaluation. A nice, compact piece of work. If you want to take your XY Plots to the next level, I recommend checking out TTokoro’s challenge worksheets.
Alan Stevens posted an economical Mathcad Express worksheet. (Since the Express version lacks the Chart Component and 3D plots, he and Fred were not able to complete questions 5 and 6.) As I had suggested in a subsequent comment, Alan considered conservation of potential energy into kinetic energy, resulting in compact equations and functions. The optimum angle was solved by defining a custom function and applying the root function.
Jan Claeys’s worksheet started off with a table of contents consisting of hyperlinks to other parts of the worksheet. The calculations were documented well with text, highlighting, and use of the equality comparison operator (like Fred and others). The calculations included symbolic evaluation, the root function, an XY Plot, and even a Solve Block (my personal favorite Mathcad functionality). Jan completed questions 5 and 6 with a very nice Chart Component and 3D Plot, then concluded the worksheet with hyperlinks to external references. Like Jeff’s, this worksheet makes a very nice teaching tool.
There were two sets of answers, depending on whether rotational inertia was taken into account. The people who submitted worksheets found those results. The more time I have worked in industry, the more I have realized the importance of documentation. It doesn’t matter how great your results are if you fail to communicate them effectively. We’re also not able to explain our results personally (especially years after the fact), so it’s important that the work stands on its own. Like previous months, we see a variety of solution tools, but also a variety of different tools to document that work. I recommend checking out the submissions to see which communication methods resonate with you to include in your own work. You can also check out all of the previous challenges and solutions that have covered a wide range of topics so far.
Get the latest Mathcad Community Challenge, plus other Mathcad tips, tricks, and more!