
The November 2022 Mathcad Community Challenge was based around kicking field goals in American football:
Create a Mathcad worksheet where you calculate the following angles from a given line of scrimmage for making a field goal:
How can you show how those angles change as a function of the line of scrimmage?
First off, mea culpa. I added a third challenge involving calculating a kick trajectory based on an old college physics problem, but I forgot to specify the initial velocity as required by the trajectory equation. I messed up worse than Matt Sanchez’s butt fumble.
Or did I…
Regular contributor Fred Kohlhepp was the first to get into the end zone. Once again, he submitted a beautiful worksheet with plenty of documentation and color. Given how screwy American football is mixing yards and feet, he was sure to incorporate units into his variables.
Fred used functions and vectors (including the Vectorize operator) to calculate the lateral (horizontal) angle within which a ball would have to be kicked through the uprights from the 20 yard line.
Then he defined a series of equations for horizontal, vertical, and total flight in order to determine the flight time. Since he is using Mathcad Express, he could not use the Solve Block construct. Instead, he used the root function to solve for time for all three equations and graphed all three in a 2D plot with a range variable.
Fred did indeed find the “shallow” angle for the trajectory of this kick but showed that the initial velocity would be more akin to a cannon than a placekicker.
Ppal, another frequent contributor, created a worksheet using the same assumptions as Fred. I had trouble following some of the logic and equations. This worksheet could use a little more documentation. It also seemed to miss the angles requested to be solved. Nice try, but the refs call this one an incomplete pass.
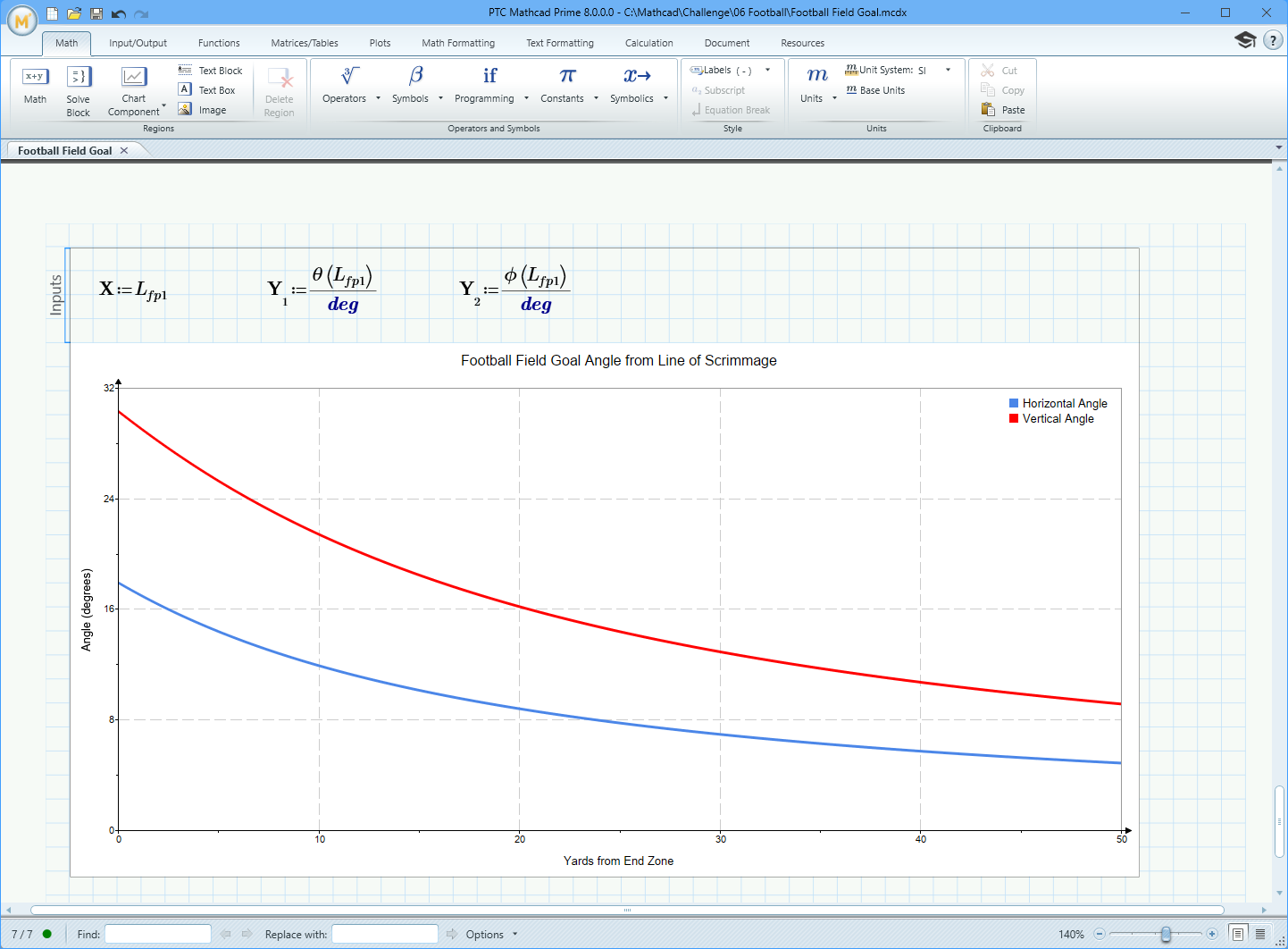
The user with the handle CP10451679 won the game though, delivering what I was looking for. They used the Law of Cosines to write a function to calculate the horizontal angle between the left and right goal posts as a function of field position. Then using a range variable, they plotted this from 0 to 100 yards.
It shows exactly the effect I wanted someone to capture. At the 0 yard line, a kicker has a window of almost 18 degrees to make the field goal. But once you get to the 50 yard line (middle of the field, where no one has ever made the kick, the window shrinks to 5.2 degrees.
Then they repeated the process for the vertical angle. At the 0 yard line, you have a 30 degree angle to kick the ball through. But at the 50 yard line, this shrinks to just under 10 degrees.
The use of plots and images in this worksheet are great. It’s important not just to solve for the answer, but to communicate the answer effectively.
Although I watch a lot of football, this problem was inspired by a frequent walk I make. Taking my little girl to school or the playground, we often cross a football field. Sometimes I start near the goalpost and walk backwards to see how the angle shrinks. It makes me respect kickers even more.
But here, our challengers have used Mathcad Prime to figure out these angles quantitatively instead of qualitatively. How can you apply Mathcad to solve problems in your everyday life?
Join us in January for another Mathcad Community Challenge!
Get the latest Mathcad Community Challenge, plus other Mathcad tips, tricks, and more!