The May 2022 Mathcad Community Challenge asked users to solve an isoperimetric problem:
Create a worksheet in which you calculate (1) the diameter of a circle and (2) the length of a side of a square that yields the minimum combined area for a combined perimeter of 1 meter. This is an optimization problem. What tools within Mathcad can provide you with a result? Optional: How can you depict the results? Can you use a 2D plot or Chart Component to visualize the answer?
Six qualifying solutions were submitted. Once again, if you have not looked at the solutions that people submitted, I strongly encourage you to do so. I guarantee you will learn something. Let’s take a look at what makes each of the submissions special.
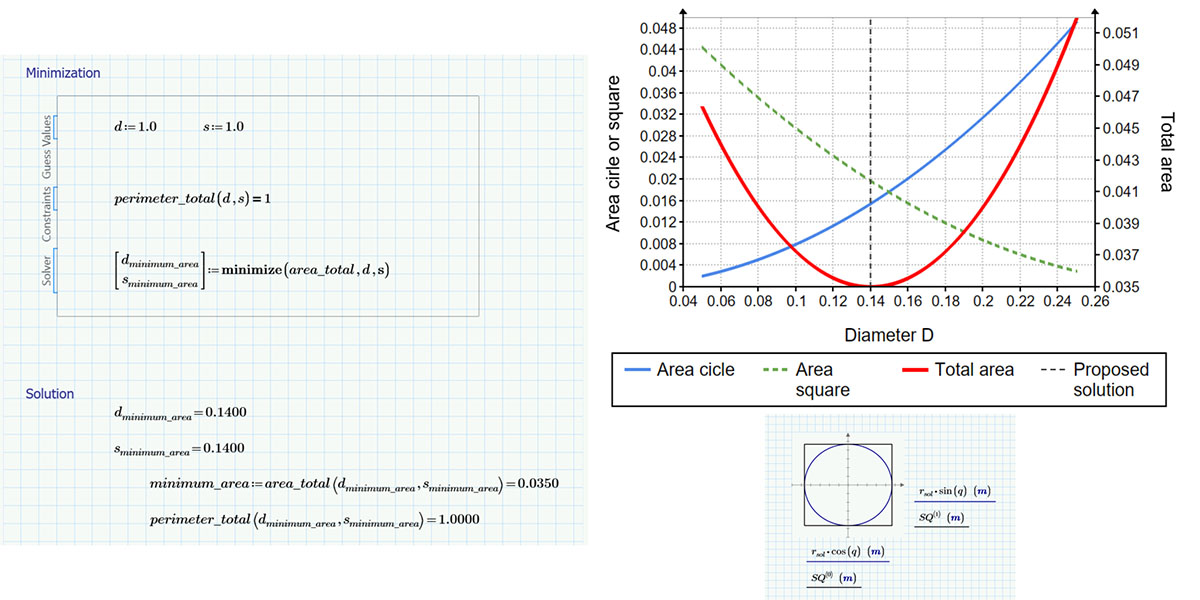
Once again, Terry was the first to respond, less than 10 hours after the challenge was posted. Terry used a Solve Block, which is the approach that immediately came to my mind for solving the problem. The Solve Block construct is my favorite tool in Mathcad because of its beauty.
Terry set up his functions. He entered his guess values, constraints, and vector to be minimized. He evaluated the results. To confirm the validity of the solution, he used a program and functions to graph the areas versus inputs on an XY Plot. Fast and correct.
The second entry by user “ppal” took a slightly different approach. They recognized that one method of finding a maximum or minimum is by evaluating the roots of the first derivative of a function. They set up user-defined functions for the perimeter and area calculations in terms of a single variable, the circle radius. Then they used the derivative operator, symbolic evaluation with the coeffs keyword, and the polyroots function.
My only quibble is that by solving for the radius instead of the diameter, they missed out on the revelation that the diameter of the circle and the length of a side of the square are equal.
User “Werner_E” remarked that he could not use symbolic evaluation due to using Mathcad Express. Therefore, he expressed the length of the side of the square in terms of the circle’s diameter; defined functions for the areas of the circle, square, and combined area; and used the root function to solve for the diameter. Another quick and elegant solution (very few functions involved), finished off with a plot of the combined area as a function of the diameter to verify a correct solution.
I liked Werner’s use of the range variable in the plot and units in the variables and functions.
After setting up variables and functions, user “TTokoro” took advantage of the new partial differential operator in Mathcad Prime 8, as well as symbolic evaluation with the solve and simplify keywords, to find the answer. They also used the Combo Box input control (introduced in Prime 7) so users could see the effect of different conditions on the resulting areas, diameter, and square side length.
TTokoro verified the calculations with two XY plots, one for the area, and another that drew the resulting circle and square.
I liked TTokoro’s extensive use of documentation and vibrant colors for both math and text regions. It helped me feel more engaged with their worksheet. Also, nice use of the Draft View to hide certain calculations.
Left: Terry's Solve Block. Top right: Bengt's chart. Bottom right: Fred's XY Plot.
Fred was our second user to solve the problem in Mathcad Express. He set up the area functions, the derivative of the area function, and a roots function to solve for the radius. I like how he documented that his XY Plot verified that the roots did indeed find the minimum value for the combined area as a function of radius. (The derivative can find a minimum or a maximum.)
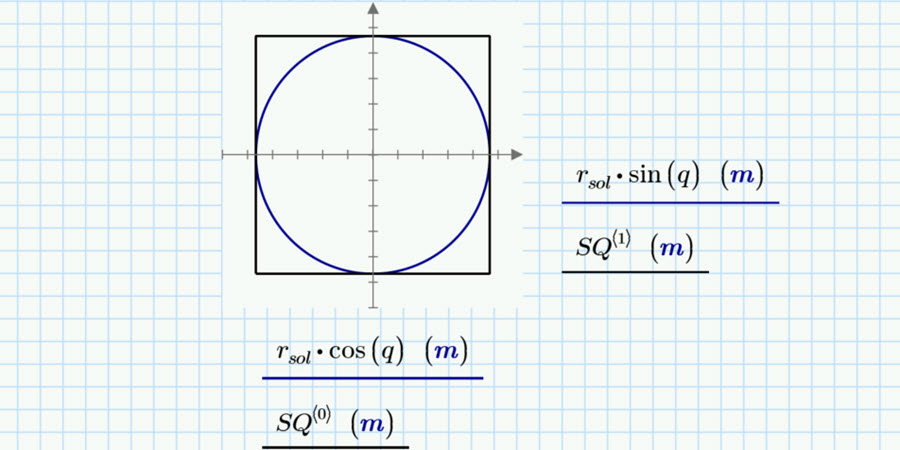
Like Ttokoro, Fred graphed the circle and square and in XY plot. I like how Fred graphed the two with the same center. This visually depicts that the solution is a circle inscribed in the square. One of the most important aspects of any study is the communication of the results to others.
Like some of the others, Bengt defined functions and performed symbolic evaluation to get to the solution. Their use of the substitute and collect keywords in the symbolic evaluation was unique. I also like the use of different colors for the text regions and math regions. Such a simple approach to differentiate between the two. I’m going to use that in my worksheets.
I especially like the text block that says, “They get equal – neat!” That’s the revelation of the isoperimetric problem: the diameter of the circle and the length of the side of the square are equal.
Bengt also was the only person to depict the results visually with the newer Chart Component tool. It’s an attractive, publication-ready graph with two y-axes, one for the areas of the circle and square, and the second for the combined area.
I’ve used Mathcad for fifteen years. I have learned something from every worksheet that has been submitted for the challenge. It might be an approach I had never used before. It might be a way of formatting or documenting the worksheet. It might be a way to depict a solution graphically.
This challenge shows the real beauty of community. People built upon each other’s solutions and discussed the approaches. Most importantly, it shows how many different tools are available to solve problems and communicate the answer.
Please take a look at the solutions and download the worksheets. If you don’t have Mathcad Prime, download the free Express version today!
Remember to stay tuned for the next Mathcad Community Challenge. Be sure to create an account at PTC Community if you haven’t already, and subscribe to the challenge index and guidelines.
You'll know whenever there is a new Mathcad Community Challenge, plus other Mathcad tips, tricks, and more!