
The March 2022 Mathcad Community Challenge was an open-ended invitation to devise a worksheet that evaluates a planetary gear system. Planetary gears are found in mechanical systems including transmissions, motors, and turbines. A planetary gear consists of a sun gear, a ring, a planet carrier, and multiple planets.

This challenge is tough because planetary gears can have different components as the input, the output, and the stationary member. Depending on the choices, the resulting gear ratio can be overdrive, reduction, or reverse reduction.
Three community members submitted solutions to the challenge: Bert, Adhariya, and Terry. If you haven’t downloaded their worksheets yet, I strongly advise that you do. I guarantee there are techniques in each of them that you can learn from. Before we talk about what they did differently, let’s talk about similarities.
Documentation. Bert and Adhariya made excellent use of Text Blocks and Text Boxes to document their solution process. Terry inserted images into his worksheet. Later, I will discuss another aspect of Terry’s worksheet that really set it apart for communicating results.
Combo Boxes. Even though the input/output Combo Box functionality was just introduced in Prime 7, Bert and Adhariya incorporated them into their solutions. Bert used three Combo Boxes to specify the Sun, Planet Carrier, and Ring as either driven, driving, or stationary. Adhariya’s Combo Box allows you to select the stationary member.
Programs. Given the open-ended problem and the various configurations, I figured it was pretty much impossible to devise any solution that didn’t use programs. Bert’s program issued a warning for an invalid configuration.
Solving for Multiple Variables Simultaneously. The Solve Block is my favorite tool in Mathcad. It’s a great construct for either solving for or optimizing variables in a system of equations. Terry used the Solve Block to calculate an angle. One thing I like about the two challenges so far is that I have learned new techniques. Adhariya used a function defined as a vector of equations, and then symbolically evaluated the system of equations using the solve keyword. Bert defined a single-row matrix as a vector of a system of equations, and then symbolically evaluated the system using the solve and float keywords to calculate rotational speeds.
Now that we’ve looked at some of the common techniques, let’s discuss some of the aspects that make each worksheet special.
Bert employs multiple vectors to define the configuration of the system, such as gear teeth, mating teeth, diameters, and rotational speeds. The vector for the diameters is constructed via the vectorize operator, which is a nice touch.
Bert then calculated the normal modules using the built-in Floor function to round a number down, and reset the variables numerically using the clear.sym function. This enabled him to complete the worksheet by calculating the number of teeth of the various members and the gear ratio. This involves some nice use of symbolic evaluation with the simplify keyword.
As mentioned above, Adhariya’s solution employed extensive text in documentation, vectors with symbolic evaluation for sets of equations, a Combo Box, and programs. It was the easiest to follow. I was expecting someone to use a program with if and else statements to compute the gear ratios based on the user-selected configuration.
One aspect I particularly liked about this spreadsheet were the Tables that symbolically defined velocities and ratios based on the stationary component. I’m rapidly discovering that Tables are an underused gem that facilitates calculations and documentation.
The third solution submitted by Terry Hendicott had something I am still trying to figure out. He used multiple traces in a 2D XY plot to depict the arrangement and intermeshing of the teeth of the sun gear, ring carrier, and planets.
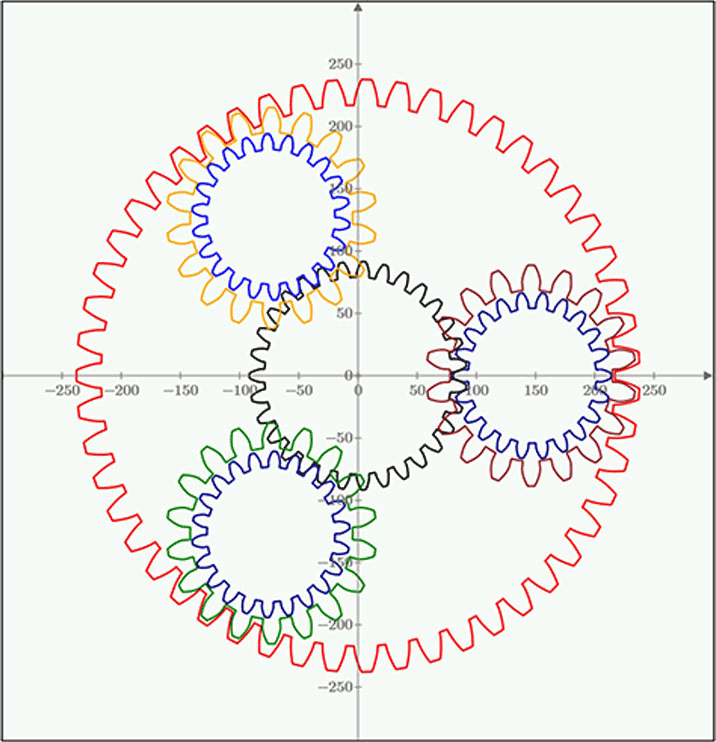
With such an open-ended problem, the variety within the three worksheets show the flexibility of Mathcad’s tools for tackling complex mechanical systems: Combo Boxes, vectors, built-in functions, programs, symbolic evaluation, and more.
Once again, I strongly recommend taking a look at the responses to learn what tools you can add to your toolbox for solving and documenting your engineering problems.
Stay tuned for the next Mathcad Challenge, which has been posted now! Be sure to create an account at PTC Community if you haven’t already and subscribe to the challenge index and guidelines.
You'll know whenever there is a new Mathcad Community Challenge, plus other Mathcad tips, tricks, and more!