PTC Mathcad Challenge 5: Resistors in Parallel

September’s Mathcad challenge was by far the most popular so far. Ten people submitted sixteen worksheets. That’s almost three times as many worksheets submitted than the previous record for a challenge. Three people submitted multiple worksheets, and one of those people built on the work of someone else’s worksheet. Exciting stuff. There was also great interaction on the PTC Community board.

Here was the problem:

We have a simple circuit with an electrical potential of 220 Volts. Initially we have a single 10 Ohm resistor. Then we add a second resistor in parallel, with 10% higher resistance. Then we add a third resistor in parallel, with 10% higher resistance than the previous resistor. And so on.

• Calculate the current in the circuit for the single resistor case.
• Calculate the resistance of each additional resistor and current through each resistor for 2, 3, 4, 5, and 10 resistors in parallel.
• Can you write a function or program that calculates the resistance of each resistor and current through each resistor for n resistors in parallel?

Confession: I am not an electrical engineer. I thought the math was going to be harder, requiring calculating the equivalent resistance. It didn’t. Therefore, the challenge really comes down to the execution. I’m grading on the methods and the presentation. How did people document and communicate their calculations?

Let’s take a look at the submissions.

Cornel Bejan responded first, using programs with for loops and the if-else construct to calculate the correct results. However, I would have liked to see more documentation. If someone else picked up the worksheet, would they understand what was being solved?

Luc Meekes then responded with a worksheet that included documentation, and elegant custom functions that are more complex than they look due to the matrix built-in function. A second worksheet used the if function, then constructed and evaluated a vector inline.

Fred Kohlhepp, another regular contributor, wrote functions for the resistance and current, but then used a transposed vector as the input, and wisely used the vectorization operator when generating the results. Neat stuff. Fred was the first to submit a worksheet that used XY plots. He depicted the trend for equivalent resistance and total current as the number of resistors increases, using a logarithmic scale.

Check out user RantEng’s worksheet. I like the use of documenting the development of the logic for computing the combined resistance, via symbolic evaluation using the substitute and factor keywords. The results are displayed in vectors as well as an XY plot.

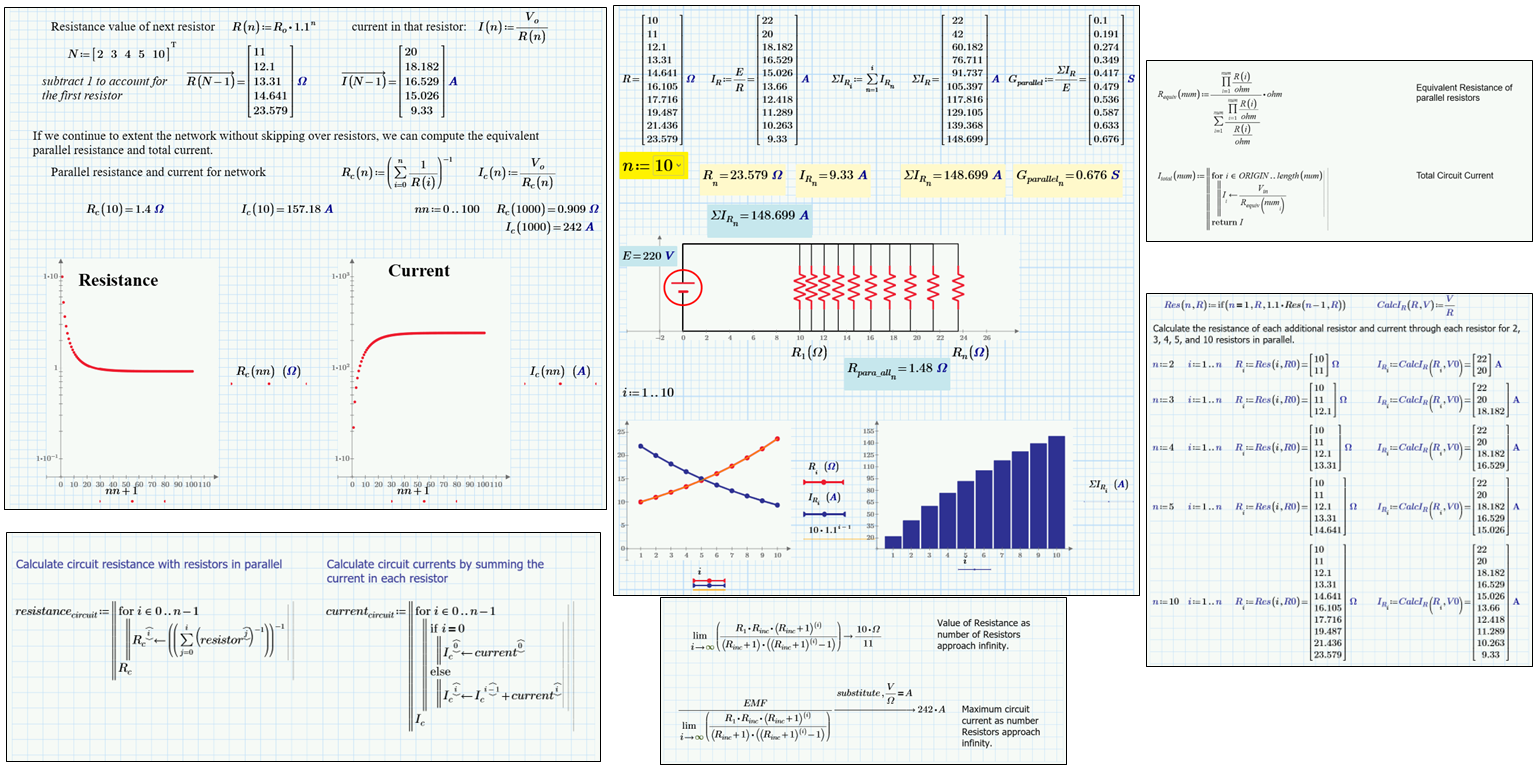
Return contributor Ppal submitted three worksheets. The first solved each case explicitly, and then with functions and vectors, displaying current in each resistor and total current in XY plots. A second used functions and vectors like the others, but was unique in that it used the limit operator and symbolic evaluation to find the resistance and current as the number of resistors approaches infinity (a built-in constant in Mathcad).

Before discussing Ppal’s third worksheet, Strib submitted a worksheet that documented a logical approach to solving the problem, including the summation operator which I don’t recall anyone else using prior. Ppal built on this approach to solve the problem numerically.

I always like the use of color and creative plots in T. Tokoro’s worksheets. Be sure to view the worksheets in Draft mode to see how those plots are constructed. The plots even depict the circuit, including resistor and battery symbols! But I also like the current versus resistance XY plot and the total current plot using a column trace.

SC_2975838 submitted two versions of the same worksheet. These two show the additional steps of calculating and plotting the power dissipation as well. There’s good use of color for the math regions, but I suggest adding text regions for documentation.

ATSchida’s worksheet had much of same approaches in earlier submissions, but also included a function for the equivalent resistance, using the product and summation operators. I’m embarrassed to admit I’ve never used the product operator. The beauty of the community challenge is being introduced to new tools. A program with a for loop calculates the total current.

The final submission by MJ_9796426 includes the image from the problem (I always like images for documentation). The solution uses programs (for scalability, as noted by MJ in a post) with for loops, summation, and several uses of the matrix row operator, something not seen in previous submissions.

I say this all the time, but every month I am amazed at the skills and techniques in the user community. The running theme is that our community uses such a wide variety of different tools available in Mathcad approaching the same problem.

Join us in November for another geometry-based challenge – this time based around American football! Subscribe to the PTC Mathcad Community Challenge Index and Guidelines thread on the PTC Community for when that challenge will be up, as well as links to the other challenges and their blog articles.