
Editor's note: This blog article has a companion PTC Mathcad Prime 8 worksheet. Download it here for additional notes for how the pictured functions and graphs were made. If you need a Mathcad Prime 8 file reader, click here.
Calculus is a branch of mathematics quantifying the change of a function. Calculus can be broken down into two main areas: derivative calculus and integral calculus. Derivatives measure the rate of change of a function. Integrals measure the area under the curve of a function. A partial derivative involves a function that is driven by multiple variables, and we find the rate of change of one variable while assuming all the other variables are held constant. If you have ever driven a car, then you can understand the basic concepts of derivatives and partial derivatives. Let’s look at a simple example.
Let’s say you are going to drive your car from your home to work. It takes time to get from point A to point B. You can use a watch to measure time and an odometer to measure distance.
You won’t drive at the same speed the entire trip. You start at rest and move faster to get to your cruising speed. Traffic may cause you to slow down. In some areas you drive faster than others. At red lights and stop signs, you have to stop entirely. Suppose we have the following simple function for the distance you drive over 10 seconds of time:
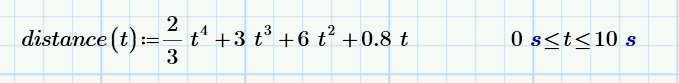
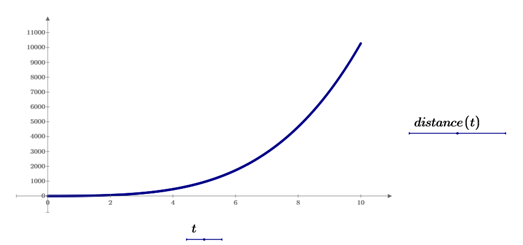
We can graph the distance along the vertical axis and graph against time on the horizontal axis over the 10 second interval.
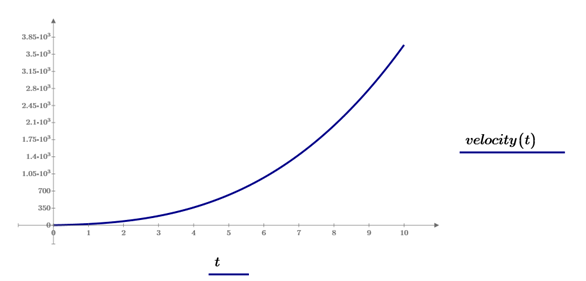
We can measure the rate of the change of our distance as the slope, or the rise over the run, of the curve. That is the derivative of our motion; the first derivative tells us about our velocity at each point of time.
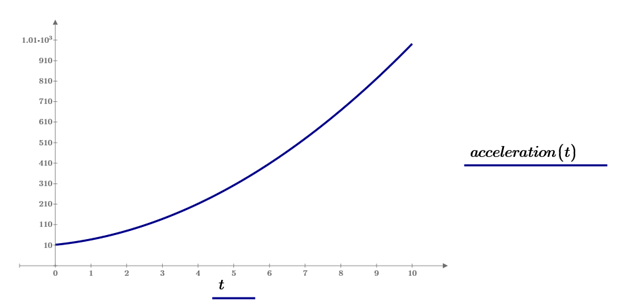
We could then take that derivative – the velocity – and graph it against time. Sometimes the velocity will increase, sometimes it will be steady, and sometimes it will decrease. If we were to measure the rate of change of our velocity over time, that’s our acceleration. The first derivative of distance is velocity, and the second derivative of distance is acceleration. In Mathcad, we can use either the standard derivative operator or the new partial derivative operator introduced starting in PTC Mathcad Prime 8 depending on preferred notation to generate the expressions for velocity and acceleration.
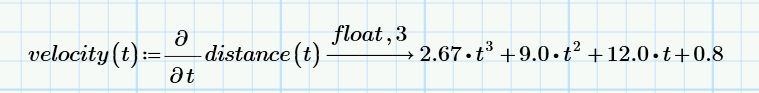
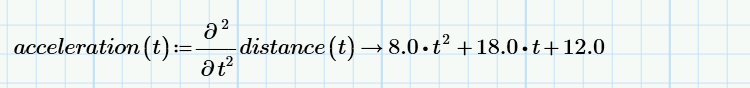
In the worlds of physics, engineering, and math, we have complicated phenomena that we want to measure. This could be fluids in motion, where position, velocity, and temperature are changing. Or the interaction of electric and magnetic fields over time, as seen in Faraday’s law of induction. Partial derivatives are used extensively in quantum mechanics, orbital mechanics, structural analysis, image processing, and even finance.
What might a partial derivative look like in our driving example? Most likely, we do not live in a straight-line path from work. We take left- and right- turns, go around bends, climb hills, and descend declines. We might formulate a function for distance traveled that involves additional variables, such as altitude. That function would incorporate both time and altitude, and we can take the partial derivative of that function with respect to either altitude or time.
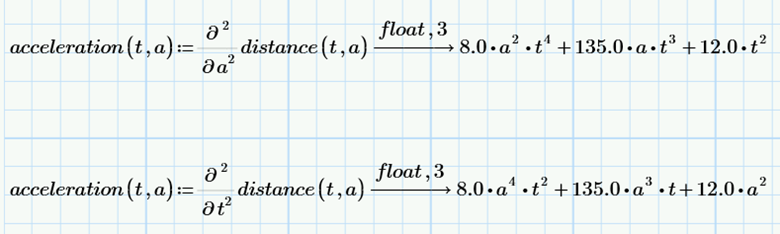
The partial derivative operator, introduced in Mathcad Prime 8, can be used to:
Mathcad Prime 8 supports up to fifth order derivatives (where functions are defined using either standard derivative notation or partial derivative notation) for numeric evaluation and any order for symbolic evaluation. Incorporating partial derivatives greatly expands the kinds of calculations you can perform.
Already a Mathcad customer? Upgrade today. Just retrieve your latest license file and download Prime 8 from support.ptc.com.
If you are not yet a customer, try Prime 8 for free for 30 days, including the new partial derivative operator.