Solving Systems of Equations in PTC Mathcad

In math and engineering, we often are left with a series of equations with an equal number of variables that we want to solve for. This is known as a system of equations. Real-world examples that require solving a system of equations include Kirchhoff’s Law for electrical resistance and aerodynamic trajectories. [That’s Kirchoff in the image above.]

PTC Mathcad has a few methods that we can use to solve for the variables. These include:

• The Solve Block construct.
• The lsolve function.
• Solving symbolically.

Let’s take a look at how to use each of these methods.

 

Solve Blocks

The Solve Block is a special structure in Mathcad. In addition to solving systems of equations, it can be used to perform optimizations – finding the minimum or maximum for a function – and differential equations. If you are going to use Mathcad for engineering calculations, I highly recommend you learn how to use this construct.

The Solve Block is initiated from the Math tab. It contains three different sections:

• Guess Values: in this section, you initialize the variables that you want to solve for using the Definition operator to assign a value. If I have no idea what to use, I will use a value of 1.
• Constraints: you write your system of equations here. Note that you use the Comparison operator, not the Evaluation operator, for the equals sign.
• Solver: create a vector for the variables you want to solve for. Then use the Definition operator to assign the Find function for the same variables.

Then outside of the Solve Block, evaluate the vector or individual variables to see the solutions.

I like Solve Blocks because they can be used to solve both linear and nonlinear systems of equations. A linear system is one in which the variables are all raised to the first power and the equation results in a line. In a nonlinear system, one or more variables are raised to a power higher than one.

Also, Mathcad will warn you if you have an inconsistent system of equations—that is, one for which a solution does not exist.

The lsolve Function

Mathcad has a built-in function for solving a linear system of equations called lsolve. To use lsolve, perform the following steps:

1. Create a matrix that contains the coefficients of the variables in your system of equations.
2. Create a vector of the constants appearing on the right-hand side of the system of equations.
3. Evaluate the lsolve function using the matrix and the vector as the inputs.

 

You can also assign the lsolve function to a variable if desired.

Symbolic Solving

Sometimes when we have a system of equations, instead of solving them numerically, we want to solve for the variables as functions of the coefficients or constants on the right-hand side of the expressions. We can do this using the Symbolic Evaluation operator and the solve keyword. After selecting the solve keyword, type in a comma followed by the variables that you want to solve symbolically:

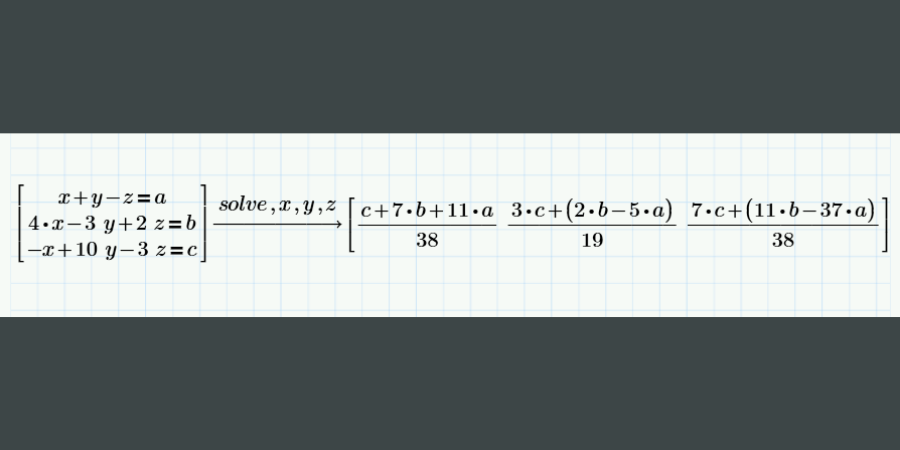
Now you have formulas for each of the variables.

Conclusion

Mathcad provides multiple methods for solving systems of equations. By familiarizing yourself with these tools, you can apply them to a variety of engineering and math problems. I especially recommend learning how to use Solve Blocks, as I have found them to be useful in many situations. Which method do you prefer?

Can you duplicate this? PTC Mathcad makes engineering calculations both easy and fun. More importantly, PTC Mathcad Express makes it free, so what are you waiting for?

 

---