
Spoiler alert for multiple comic book movies.
I've loved comic books since junior high and I absolutely love movies based on comic books. But I can't turn off the engineer side of me and thinking about physics. There's a common scene in many superhero movies where someone is falling and the hero catches them. Most notably I'm thinking about Superman catching Lois Lane in “Superman: The Movie” from 1977, but it happens all over the place:
Every time I see that happen in the movies, I think "They're still dead." Based on physics, the superhero actually makes things worse. All the force is distributed over less surface area, resulting in higher stress. About the only movie that got this realistic was “The Amazing Spider-Man 2” when Gwen Stacy died. (In the movie she actually bounced off the ground, but in the comic book she broke her neck in mid-air.)
Despite what happened to Gwen Stacy, I appreciate the way that Spider-Man’s webbing has been depicted on film since 2002. It’s very elastic, dissipating force and energy, allowing your favorite wall-crawler to save people.
True believers, let’s use PTC Mathcad to calculate the safe negative acceleration to restrain the fall of a human. I am going to use the example of Superman catching Lois Lane as she falls from a 50-story height and Superman catches her halfway down. You can see my assumptions and analysis here:

Great Caesar’s ghost! From a purely stress analysis standpoint, with the criteria being that the stress on Lois Lane should be less than the yield stress of bone, it turns out that Lois should be okay!
But we are more than bones, and just because you don’t break bones doesn’t mean that you won’t be injured or worse. Analysis into falls and jolts shows that there are maximum limits to acceleration that the human body should experience:
(G is the acceleration due to gravity, which is approximately 32.2 feet per second squared at the earth's surface.)
In the initial analysis, Lois Lane was subjected to an acceleration of 45 G’s. In other words, Superman’s catch most likely would have been fatal. If Superman wants to save Lois from falling, he should fly from the ground past her, change direction, match her speed and position, then start slowing down her fall - not immediately stop her.
We can use an equation to calculate the acceleration in G’s based on the stopping distance:

Alternatively, we can rearrange the equation in order to calculate the safe stopping distance as a function of desired acceleration (deceleration):

Similarly, we can use equations of motion for constant acceleration to calculate the time that this deceleration will take, and the subsequent resulting force applied to Lois Lane. This turns out to be 0.753 seconds, or just over three quarters of a second.
Using PTC Mathcad’s Chart Component functionality, we can graph the acceleration as a function of stopping time:
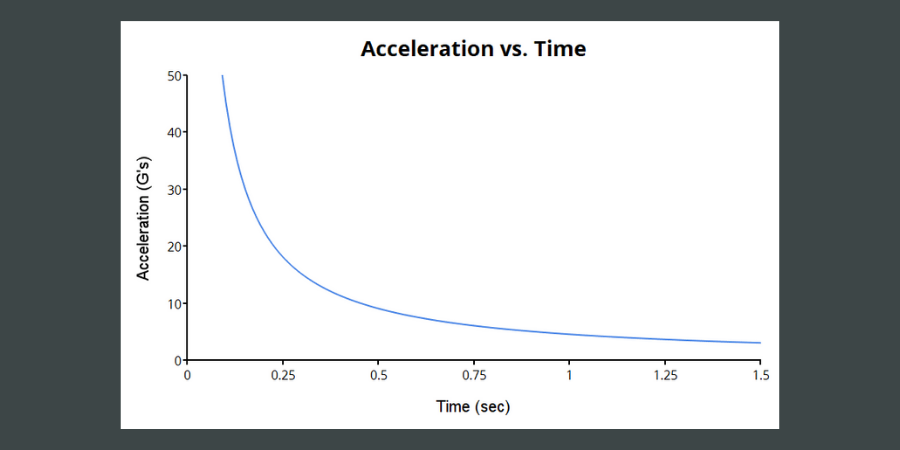
What do we learn from all this? If you’re a superhero, the key to avoiding injuring the person you’re trying to save is not to catch them mid-air, but to slow down their fall over as long a distance and time as possible.
Excelsior!
PTC Mathcad is used by professional scientists and engineers to solve complex technical problems in ways that are easy to visualize and much more. Check out Dave Martin’s eBook When Spreadsheets Fall Short: A Guide to Smarter Engineering Calculations to learn more.