
Editor's note: This blog article was originally written as a PTC Mathcad Prime worksheet. For the best reading experience, please download the Mathcad Prime 8 worksheet here. If you need a Mathcad Prime worksheet viewer, download Mathcad Prime for free here.
My sons and I like to explore the western deserts of Utah. We often come across deep vertical mine shafts that have been covered by a gridwork of bars that allow you to walk out directly over the shaft. We like to drop a rock and time how long it takes for the rock to hit the bottom of the shaft. We use the physics equation, d = ½a*t² , to calculate the depth of the shaft. Because we are in the desert without a computer, we neglect the time it takes for the sound to get from the bottom of the shaft up to our ears, and we neglect the air resistance on the rock.
We know that the acceleration of gravity is 32.174ft/s². Once we know the time, we can calculate the depth of the shaft. This blog will look at three different ways to solve this simple problem to look at the power of PTC Mathcad Prime.
Problem:
Calculate the depth of the shaft if it takes 5.5 seconds to hear the rock hit the bottom of the shaft.
We will first use Mathcad as a calculator. Since this equation involves units, we will also attach units. Mathcad also has a built-in variable (g = 32.174 ft/s²) so we will use that as well.
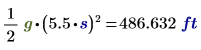
Next, let's assign variables to distance and time.

Since Mathcad is unit aware, we can also display the distance in meters.
Now that we have the time assigned to a variable, we can change the variable and recalculate the distance.

Note the green boxes around "t" and "Distance". Beginning with Mathcad Prime 8, Mathcad alerts you when you redefine a variable, as we just did in this example.
Finally, we will create a function for this problem. We will call the function "Depth" with a variable of time (t). The function is very simple to create. Simply define the variable and then list the inputs to the function in parenthesis, and then tell Mathcad the equation using the input variables.
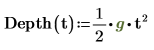
This function is "Depth" as a function of time. Because the function uses the input "t", it uses the value of "t" when it sees it in the equation; it does not use the defined value of "t" defined above.
Now that we have the function created, all we need to do is type the equation and then put the value of t in parenthesis. Remember to attach the units of seconds to the input.
This allows you to quickly test several variables of time.
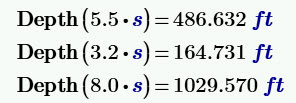
You can also assign a variable to the results of the function.

This example was rather simple, but hopefully it helps illustrate the ease and power of Mathcad, especially the power and ease of user-defined functions.
Let's now make the problem a bit more complicated by considering how long it takes for the sound to come up from the bottom of the shaft to your ears.
The velocity of sound is about 1,125 ft/s (343 m/s) at 68 degrees F (20 C), so let's use this value.
We now have a problem of not knowing how deep the hole is, so we cannot calculate how long it takes for sound to get up to your ears. This is an iterative problem. A future blog will illustrate how to use Mathcad's solving feature, but for this blog we will just manually iterate a solution.
In order to do this, we need to subtract the time it takes for the sound to come up the shaft. We can do this in the function's definition of time.

Here, Brent compares the input depth versus the calculated depth across multiple guess values, changing the depth after looking at the results.
This is for the time being 5 seconds, 3.2 seconds, and 8 seconds.
Note how the calculated depth of the shaft changed, once the time it takes for the sound to come up the shaft is considered, especially for the deeper shafts.
This blog shows how easy it is to use Mathcad as a simple calculator (good) and how to assign variables to equations (better), but the real power of Mathcad is illustrated by the use of user-defined functions (best).
Try creating a few functions for your most often used equations.
Download and install the full Mathcad Prime for 30 days to try out the best of Mathcad for yourself.