Solving Iterative Problems

Editor's note: This blog article was originally written as a PTC Mathcad Prime worksheet. For the best reading experience, please download the Mathcad Prime 8 worksheet here. If you need a Mathcad Prime worksheet viewer, download Mathcad Prime for free here.

In my last blog, I discussed calculating the depth of a vertical mine shaft by timing how long it took for a rock to drop to the bottom. When the time it takes for the sound to come up to the surface it required some iteration to find the depth of the shaft.

In this blog I will discuss how to use the powerful solving features of Mathcad to directly calculate the depth of the shaft from the measured time.

Just as in the last blog, I will illustrate different ways of solving this problem.

Recap: The depth of a mine shaft can be calculated by timing how long it takes a rock to fall (neglecting air resistance) by using the equation: d = ½a*t²

If you are standing at the surface recording the time, you must subtract the time it takes for the sound to get from the bottom of the shaft up to your ears. But, this is a function of the depth of the shaft, which you don't know.

We will look at this problem differently than in the last blog. We will write an equation for how long it takes the sound to get to your ears as a function of depth. The first part of the equation will calculate the time it takes for the rock to hit the bottom of the shaft, and the second part of the equation will calculate how long it takes for the sound to get from the bottom of the shaft up to your ears.

Introducing the Solve Function

Part 1: Calculate the time it takes for the rock to hit the bottom of the shaft.

We could solve for time by simple algebra, but I want to illustrate the solve function, which will be discussed in more depth in a future blog. (On the Math tab, in the Operators group, select Symbolics and select the solve keyword.) Type a "t" to solve for time.

Because this is a quadratic equation, we get two solutions, one of which results in negative time.

Part 2: Calculate the time it takes for the sound to get to the surface.

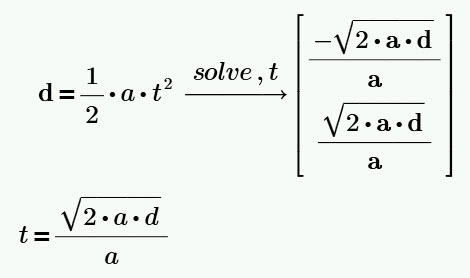
The time it takes for sound to get to the surface is the depth of the shaft divided by the velocity of sound. As in the previous example, we will use a velocity of sound of about 1125 ft/s (343 m/s) at 68 degrees F (20 C).

Let's look at two ways to solve this problem.

Using a Solve Block

The first solution uses a solve block. Add a solve block from the Math tab, Regions group. There are three parts to the solve block. The first is a guess value. The second is a constraint section, and the third section is the solver section using the find function (additional functions available for use in the solver section are listed under the Functions/Solving category).

Input the measured time. (This is the time it takes for the rock to hit the bottom plus the time it takes for sound to get to the surface.)

A solve block iterates until it finds a solution for the requested variable(s) that satisfies the constraints.

Let's set Measured Time to 5.5 seconds. MeasuredTime:= 5.5s

This value of d is only a guess value to start the iteration.

Constraints are the relationships between variables. In this case, it is the relationship between measured time and depth.
For a solve block use ctrl + = to set the relationship

The find function solves for the variable in parenthesis.

The depth is equal to 422.451 feet, or 128.763 meters. This solution is consistent with the manual iteration from the previous blog.

Now let's set Measured Time to 8 seconds. MeasuredTime:= 8s

Guess value

This is the relationship between measured time and depth.

The find function solves for the variable in parenthesis.

At a Measured Time of 8 seconds, the depth is equal to 845.261 feet, or 257.636 meters. This solution is consistent with the previous blog.

Creating a Function Using the Solve Keyword

The second method to solve this problem is to create a function that will provide a direct solution using the solve keyword. The solve keyword is part of Mathcad's symbolic engine.

Note: In this example I have customized the appearance of function names. This is an easy two-step process:

1. On the Math Formatting tab in the "Label Styles" section, I selected Function from the dropdown choices to set my visual preferences for function names. I changed the color and applied italics and underlining.
2. I put my cursor on the function name (Depth or ShaftDepth), and from the Math tab in the "Style" section, I selected "Function" from the Labels dropdown choices and applied that label style to the function name.

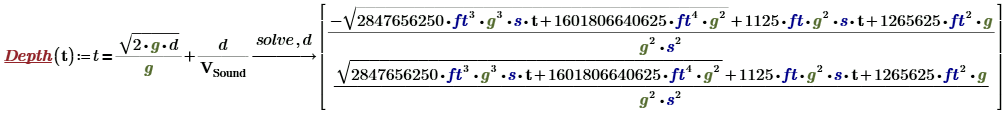
Test the function for a measured time of 8 seconds.

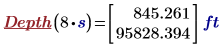
Note that there are two solutions. The larger value of depth is from a negative value of time and can be ignored.

To avoid seeing both values, modify the function to select the minimum value of depth by using the min function.

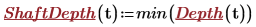
Now that you have created a function to calculate the depth of the shaft, you can simply enter the measured time and get a direct solution of shaft depth. Remember to assign the "Function" label and be sure to assign the units of seconds to the input.

This blog, as in my previous blog, illustrates the power of creating use-defined function. In this blog, we combined the power of Mathcad's powerful solving features, with the power of user-defined functions to allow a direct solution to an iterative problem.