A Program for Generating Prime Numbers in Mathcad

Editor's note: Finding prime numbers in Mathcad can be done with just a few programming steps. Dave Martin shows you how (and assures us that you don’t need much coding experience to figure it out).

If a number is divisible by exactly two numbers, the number one and the number itself, it is known as a prime number.

Prime numbers have fascinated mathematicians for thousands of years. Around 300 BC, Euclid proved there are an infinite number of prime numbers. A century later, the Greek mathematician Erastosthenes (more on him later) devised a method for finding prime numbers that bears his name today: The Sieve of Erastothenes. Great mathematicians like Euler, Escott, Fermat, and Mersenne have worked on formulas for finding prime numbers.

The Fundamental Theorem of Arithmetic states that every integer can be written as factors of prime numbers. The Goldfarb Conjecture states that every even integer can be written as the sum of two prime numbers. This hasn’t been proved for all even numbers, but it hasn’t been disproved. So there’s something inherently special about primes.

You might not know it, but prime numbers have an effect on your life every day. Every single financial transaction we do online or with our ATM cards depends on public key cryptosystems, which use incredibly long prime numbers.

One day I was thinking about prime numbers and I realized that if a number isn’t divisible by any of the numbers below its square root, it’s a prime number.

Later I learned that Erastosthenes figured that out over 2200 years ago. In fact, his sieve shows that an integer is prime if it isn’t divisible by any of the prime numbers below its square root.

I decided to see if I could write a program in Mathcad for prime numbers. Rather than determine if a number is prime or not, to make it interesting, I wanted to send a range of numbers as inputs to the program and then have it output a vector of all the prime numbers in that range. Here is the program:

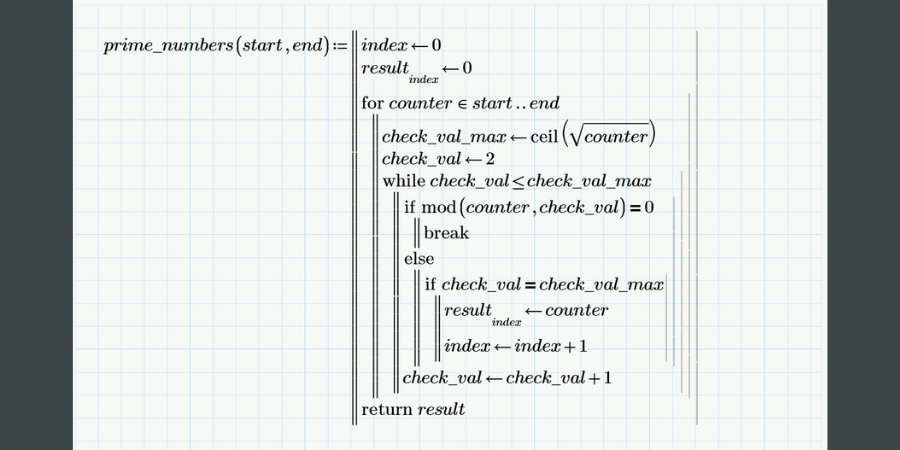
Let’s take a look at some of the aspects of this program:

• Looping is one of the most powerful aspects of a program, and this one uses two. A for loop allows you to perform a series of actions a specified number of times. A while loop repeats the actions until a certain condition is no longer true.
• The if-then-else construct evaluates a condition and performs different actions based on whether the condition is true or false.
• When a number is determined not to be a prime number, the break operator allows the program to exit the current loop and evaluate the next integer.
• It uses built-in functions like ceil to round a number up to the next integer and mod to calculate a modulus (the remainder when one number is divided by another). PTC Mathcad Prime has over 400 built-in functions in a variety of different areas.
• The program constructs a vector and returns it as a result. The program doesn’t know how big the vector will be when it is created.

Not bad for fourteen lines. Also, I am terrible at regular computer programming. I read a book on Python years ago but never made it much farther than the “Hello, World!” program. The last programming class I took was in C – not C++, regular C – back when Bush was president. The first one, not W. I’m proof that you don’t have to be good at computer programming to program in PTC Mathcad Prime.

Here are some outputs:

The program could probably be made shorter. It can definitely be made better. Programs support recursion; a program can call itself. I can make the program more efficient by incorporating recursion to compare an integer only to the prime numbers below the square root of that integer. But that’s a project for another time.

What can you do with programs to facilitate your engineering calculations? The possibilities are infinite, just like prime numbers.

---