
Editor's note: This blog article was originally written as a PTC Mathcad Prime worksheet. For the best reading experience, please download the Mathcad Prime 8 worksheet here. If you need a Mathcad Prime worksheet viewer, download Mathcad Prime for free here.
In my previous blog, I showed how to create and use functions to calculate and plot shear and bending moment diagrams for uniform load, triangular load, and point loads.
In this blog, I will show how to derive functions that will provide the maximum moment for these three loading conditions.
Most structural engineers know that for a uniformly loaded beam, the maximum moment occurs at mid-span and the value of the moment is (w*l2)/8. For a point load at the center, the maximum moment is (P*l)/4. If the load is not centered, the maximum moment is (P*a*b)/l and it occurs at the location of the point load. For a triangle load the maximum moment is located at (√3 *l)/3 and it is (√3 *w*l2)/27.
Below are the functions derived in my previous blog.
Calculating uniform load:

Calculating point load:

Calculating triangular load:

Let's first derive the function for maximum moment for a uniformly loaded beam.
Notice from the plot below that the maximum moment occurs at the location where the shear is zero. The shear is equal to the slope of the moment curve, and the slope is zero at the point of maximum moment.
We will use numeric data to plot the shear and moment diagrams and then use this data to find the maximum moment. This data will then be compared to the derived function for maximum moment as a check.
Note that the Vectorization operator is required to have Mathcad perform the calculations on an element-by-element basis. Refer to the previous blog for a discussion of the Vectorization operator.
The location of maximum moment will be calculated in two ways. The first is to use the derived shear function and solve for location where shear is zero. The second way is to take the derivative of the moment function to get a slope function (which is the same as the shear function), and then solve for the location of zero slope. The Derivative operator is located on the Math tab in the Operators section.
The location function for zero shear (and also zero slope) will then be used as the input value of x in the moment function, which will then provide the function for maximum moment.
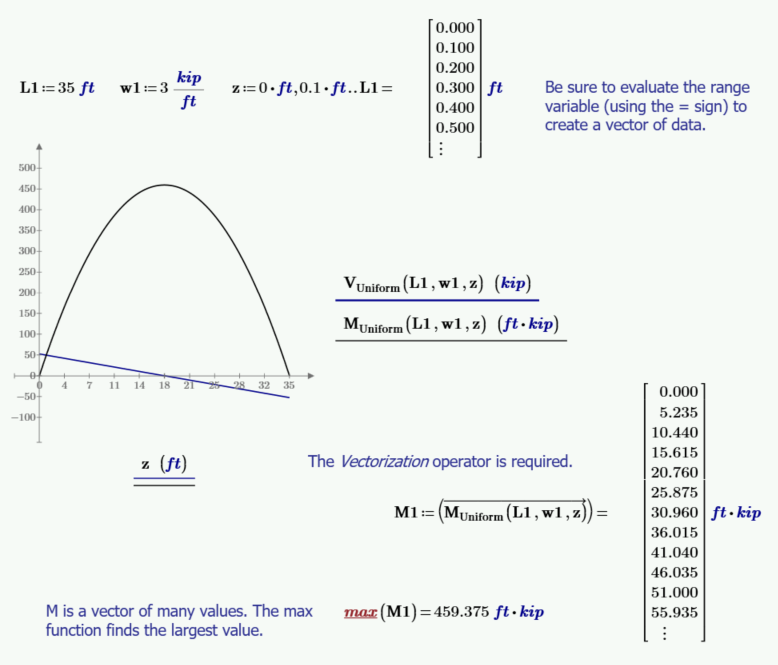
To derive the formula for the maximum moment for a uniformly loaded bean, find the location of zero shear. Use the symbolic solve keyword to find the location of zero shear.

Use the derived function with the numeric values above to check the function of the maximum moment.

Derive the function for maximum moment for a point load. The maximum moment for a beam with a point load will occur at the location of the point load.


Use the MMaxPoint function to derive the formula for point load centered in a span.

Derive the function for maximum moment for a beam with a triangular load.

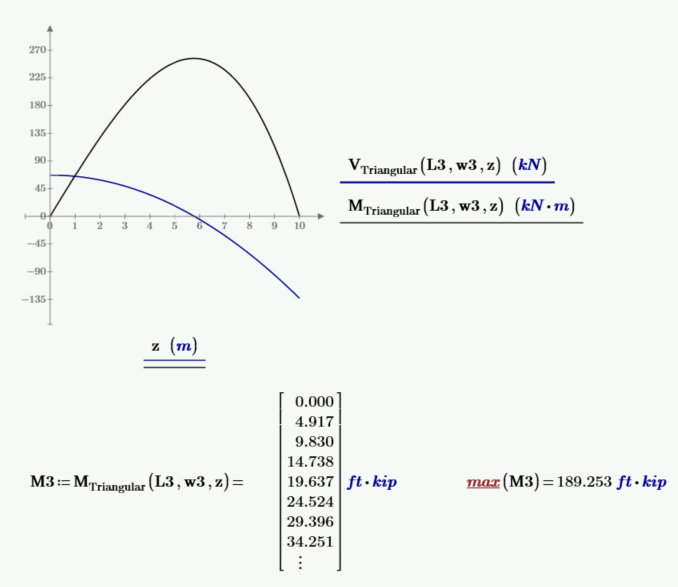

Use the derived function with the numeric values above to check the result of the maximum moment.

In this blog, I have showed how Mathcad can be used to derive functions for the maximum moment on simply supported beams with uniform load, point load, and triangular load. These examples illustrate:
Download a free 30-day trial of Mathcad Prime to see the best of Mathcad for yourself.